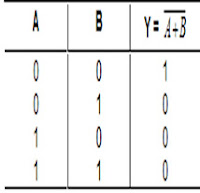
Table Operator Logika

Gerbang logika atau gerbang logik adalah suatu entitas dalam elektronika dan matematika boolean yang mengubah satu atau beberapa masukan logik menjadi sebuah sinyal keluaran logik. Gerbang logika terutama diimplementasikan secara elektronis menggunakan dioda atau transistor, akan tetapi dapat pula dibangun menggunakan susunan komponen-komponen yang memanfaatkan sifat-sifat elektromagnetik (relay). Logika merupakan dasar dari semua penalaran (reasoning). Untuk menyatukan beberapa logika, kita membutuhkan operator logika dan untuk membuktikan kebenaran dari logika, kita dapat menggunakan tabel kebenaran. Tabel kebenaran menampilkan hubungan antara nilai kebenaran dari proposisi atomik. Dengan tabel kebenaran, suatu persamaan logika ataupun proposisi bisa dicari nilai kebenarannya. Tabel kebenaran pasti mempunyai banyak aplikasi yang dapat diterapkan karena mempunyai fungsi tersebut. Salah satu dari aplikasi tersebut yaitu dengan menggunakan tabel kebenaran kita dapat mendesain suatu rangkaian logika. Dalam makalah ini akan dijelaskan bagaimana peran dan kegunaan tabel kebenaran dalam proses pendesainan suatu rangkaian logika.
Gerbang yang diterjemahkan dari istilah asing gate, adalah elemen dasar dari semua rangkaian yang menggunakan sistem digital. Semua fungsi digital pada dasarnya tersusun atas gabungan beberapa gerbang logika dasar yang disusun berdasarkan fungsi yang diinginkan. Gerbang -gerbang dasar ini bekerja atas dasar logika tegangan yang digunakan dalam teknik digital.Logika tegangan adalah asas dasar bagi gerbang-gerbang logika. Dalam teknik digital apa yang dinamakan logika tegangan adalah dua kondisi tegangan yang saling berlawanan. Kondisi tegangan “ada tegangan” mempunyai istilah lain “berlogika satu” (1) atau “berlogika tinggi” (high), sedangkan “tidak ada tegangan” memiliki istilah lain “berlogika nol” (0) atau “berlogika rendah” (low). Dalam membuat rangkaian logika kita menggunakan gerbang-gerbang logika yang sesuai dengan yang dibutuhkan. Rangkaian digital adalah sistem yang mempresentasikan sinyal sebagai nilai diskrit. Dalam sebuah sirkuit digital,sinyal direpresentasikan dengan satu dari dua macam kondisi yaitu 1 (high, active, true,) dan 0 (low, nonactive,false).” (Sendra, Smith, Keneth C)
Rangkaian Terpadu (IC) Untuk Gerbang -Gerbang Dasar
Setelah mengenal gerbang-gerbang dasar yang digunakan dalam teknik digital, bagi para pemula mengkin saja timbul pertanyaan dimana gerbang-gerbang ini dapat diperoleh? Jawabannya mudah sekali, karena gerbang- gerbang ini telah dijual secara luas dipasaran dalam IC tunggal (single chip). Yang perlu diperhatikan sekarang adalah dari jenis apa dan bagaimana penggunaan dari kaki-kaki IC yang telah didapat. Sebenarnya informasi dari IC-IC yang ada dapat dengan mudah ditemukan dalam buku data sheet IC yang sekarang ini banyak dijual. Namun sedikit contoh berikut mungkin akan me mpermudah pencarian. Berikut adalah keterangan mengenai IC-IC yang mengandung gerbang-gerbang logika dasar yang dengan mudah dapat dijumpai dipasaran.
Catatan:
Ada dua golongan besar IC yang umum digunakan yaitu TTL dan CMOS.
IC dari jenis TTL memiliki mutu yang relatif lebih baik daripada CMOS dalam hal daya yang dibutuhkan dan kekebalannya akan desah.
IC TTL membutuhkan catu tegangan sebesar 5 V sedangkan CMOS dapat diberi catu tegangan mulai 8 V sampai 15 V. Hali ini harus diingat benar-benar karena kesalahan pemberian catu akan merusakkan IC.
Karena adanya perbedaan tegangan catu maka tingkat tegangan logika juga akan berbeda. Untuk TTL logika satu diwakili oleh tegangan sebesar maksimal 5 V sedangkan untuk CMOS diwakili oleh tegangan yang maksimalnya sebesar catu yang diberikan, bila catu yang diberikan adalah 15 V maka logika satu akan diwakili oleh tegangan maksimal sebesar 15 V. Logika pada TTL dan CMOS adalah suatu tegangan yang harganya mendekati nol.
Untuk TTL nama IC yang biasanya terdiri atas susunan angka dimulai dengan angka 74 atau 54 sedangkan untuk CMOS angka ini diawali dengan 40.”(Ian Robertson Sinclair, Suryawan)
Sistem digital merupakan basis dalam melaksanakan berbagai tugaskomputasional, oleh karena itu perlu dilakukan manipulasi informasi biner dengan menggunakan rangkaian-rangkaian logika yang disebut gerbang-gerbang (gates). Gerbang didefinisikan sebagai blok-blok piranti keras (hardware) yang menghasilkan sinyal-sinyal biner; 1 atau 0, jika persyaratan-persyaratan input logika dipenuhi. Hubungan input dan output dari variabel biner untuk setiap gerbang dapat disajikan dalam sebuah tabel yang disebut “tabel kebenaran” (truth table). Gerbang-gerbang logika yang dibahas ini adalah AND, OR, NOT, NAND, NOR dan X-OR
A. Gerbang AND
Gerbang AND dinyatakan sebagai Y = A • B, dimana output rangkaian Y bernilai 1, hanya jika kedua inputnya A dan B masing-masing bernilai 1; dan output Y bernilai 0 untuk nilai-nilai A dan B yang lain. Simbol gerbang AND dapat dilihat pada Gambar 1.
 |
| Simbol Gerbang AND |
Sedangkan tabel kebenaran untuk rangkaian gerbang AND adalah:
Tabel 1. Tabel kebenaran dari gerbang AND
B. Gerbang OR
Gerbang OR dinyatakan sebagai Y = A + B, dimana output rangkaian Y bernilai 0, hanya jika kedua inputnya A dan B masing-masing bernilai 0; dan output Y bernilai 1 untuk nilai-nilai A dan B yang lain. Simbol gerbang OR dapat dilihat pada Gambar 2.
 |
| Simbol gerbang OR |
Adapun tabel kebenaran untuk rangkaian gerbang OR, sebagai berikut:
Tabel 2. Tabel kebenaran dari gerbang OR
C. Gerbang NOT
Gerbang NOT juga dikenal sebagai inverter dan dinyatakan sebagai Y = . Nilai output Y merupakan negasi atau komplemen dari input A. Jika input A bernilai 1, maka output Y bernilai 0, demikian sebaliknya. Simbol gerbang NOT dapat dilihat pada Gambar 3.
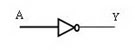 |
| Simbol gerbang NOT |
Sedangkan tabel kebenaran untuk rangkaian gerbang NOT adalah:
Tabel 3. Tabel kebenaran dari gerbang NOT
D. Gerbang NAND
Gerbang NAND dinyatakan sebagai Y =A • B , dimana output rangkaian Y bernilai 0, hanya jika kedua inputnya A dan B masing-masing bernilai 1; dan output Y bernilai 1 untuk nilai-nilai A dan B yang lain. Jadi NAND adalah komplemen dari AND. Simbol gerbang NAND dapat dilihat pada Gambar 4.
 |
| Simbol gerbang NAND |
Adapun tabel kebenaran untuk rangkaian gerbang NAND, sebagai berikut:
Tabel 4. Tabel kebenaran dari gerbang NAND
E. Gerbang NOR
Gerbang NOR dinyatakan sebagai Y =A + B , dimana output rangkaian Y
bernilai 1, hanya jika kedua inputnya A dan B masing-masing bernilai 0, dan output Y bernilai 0 untuk nilai-nilai A dan B yang lain. Jadi NOR adalah komplemen dari OR. Simbol gerbang NOR dapat dilihat pada Gambar 5.
 |
| Simbol gerbang NOR |
Sedangkan tabel kebenaran untuk rangkaian gerbang NOR adalah:
Tabel 5. Tabel kebenaran dari gerbang NOR
F. Gerbang X-ORGerbang X-OR dinyatakan sebagai Y = A • B + A• B atau disederhanakan menjadi Y = A + B, dimana output rangkaian Y bernilai 0, jika kedua input A dan B memiliki nilai yang sama, dan output Y bernilai 1 jika kedua input A dan B memiliki nilai yang tidak sama. Simbol gerbang X-OR dapat dilihat pada Gambar 6.
 |
| Simbol gerbang X-OR |
Sedangkan tabel kebenaran untuk rangkaian gerbang X-OR adalah:
Tabel 4. Tabel kebenaran dari gerbang X-OR